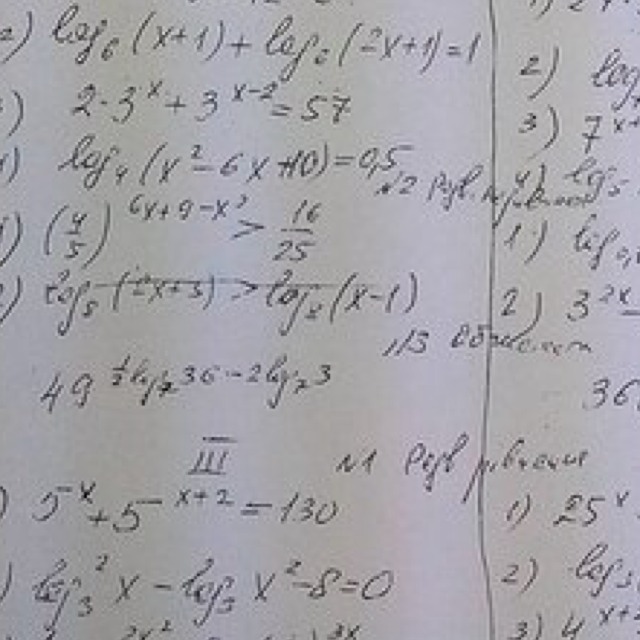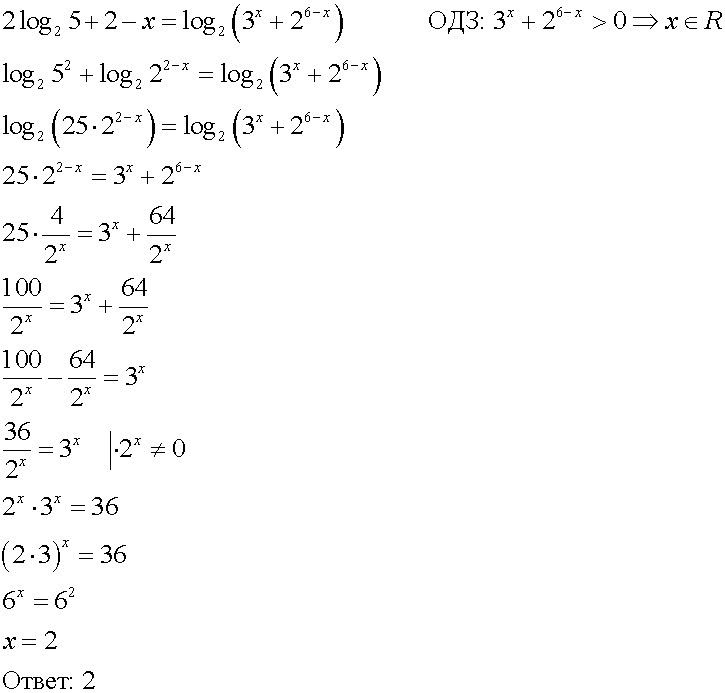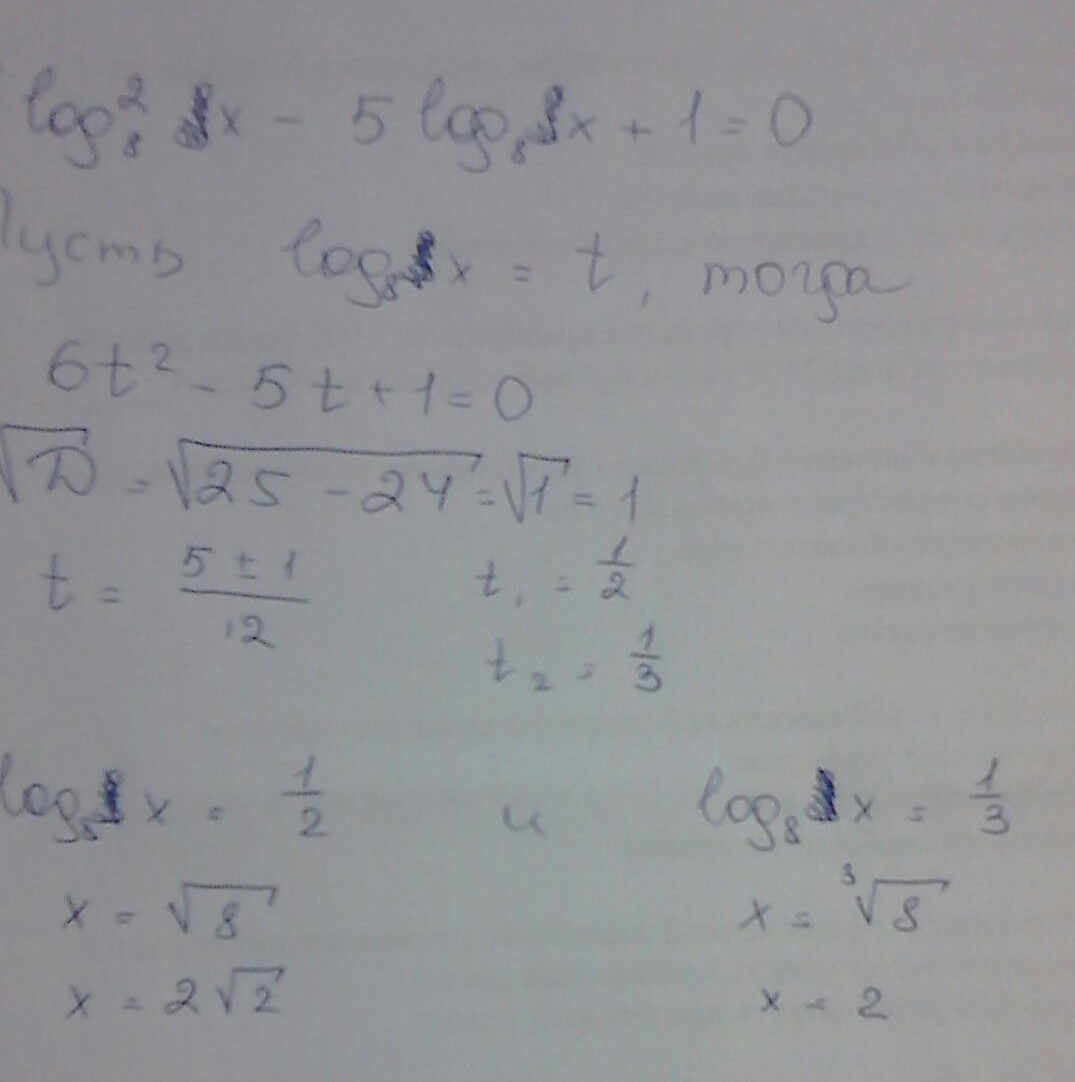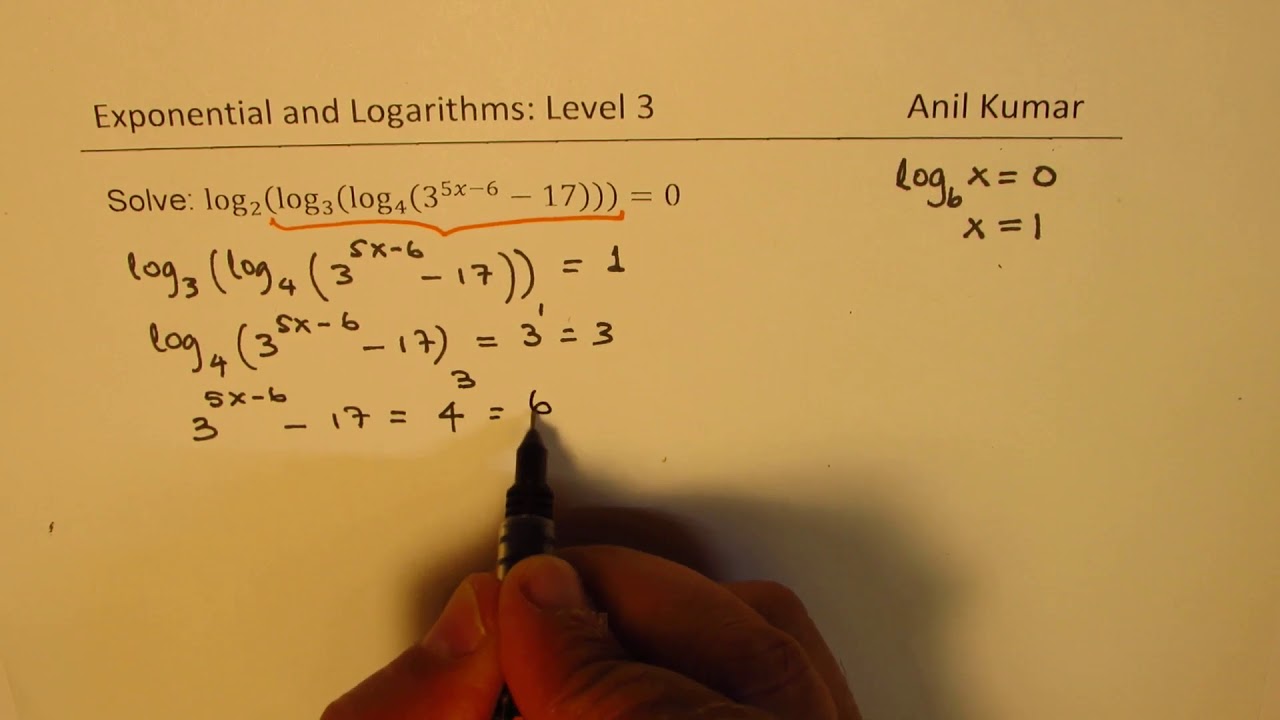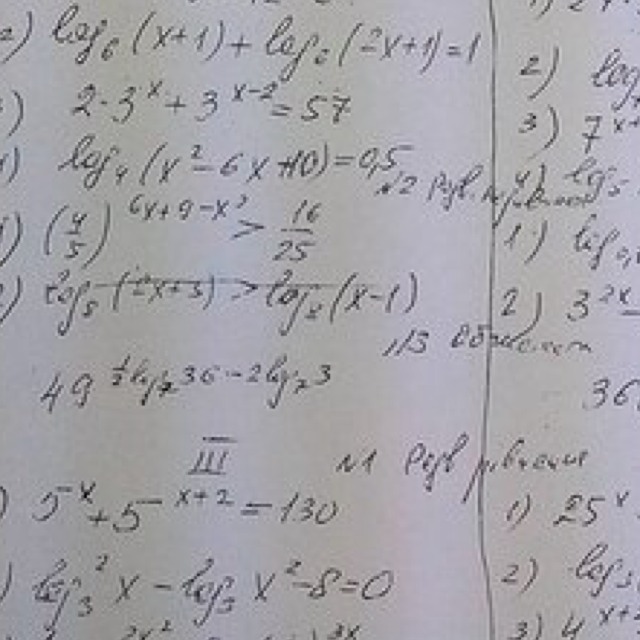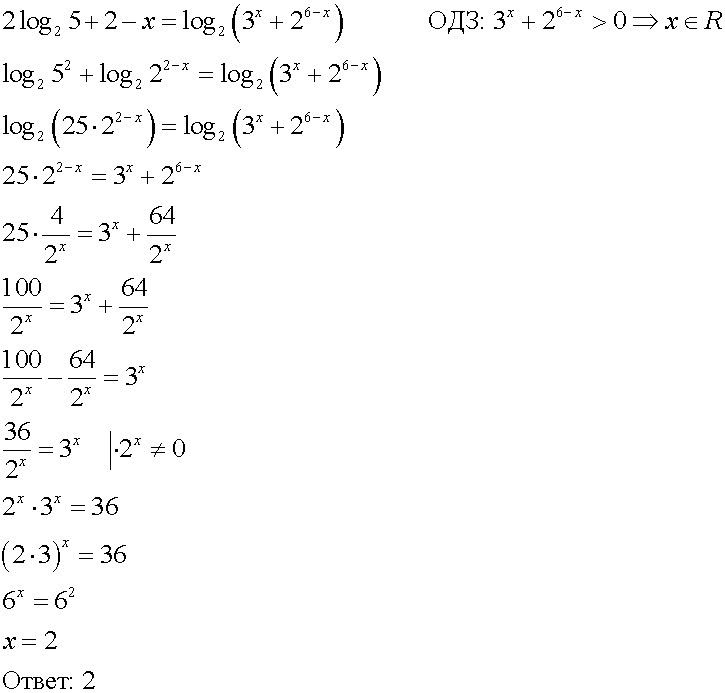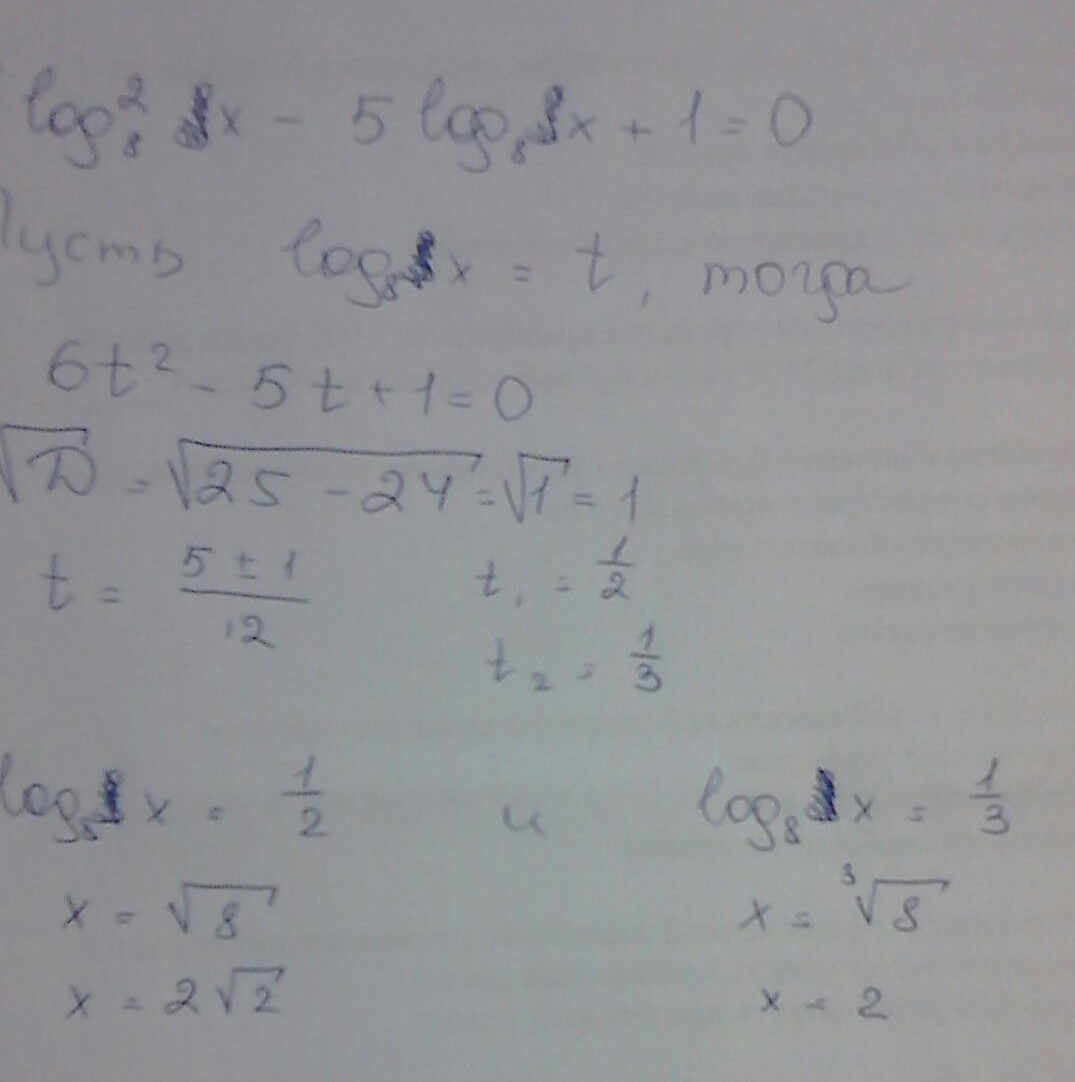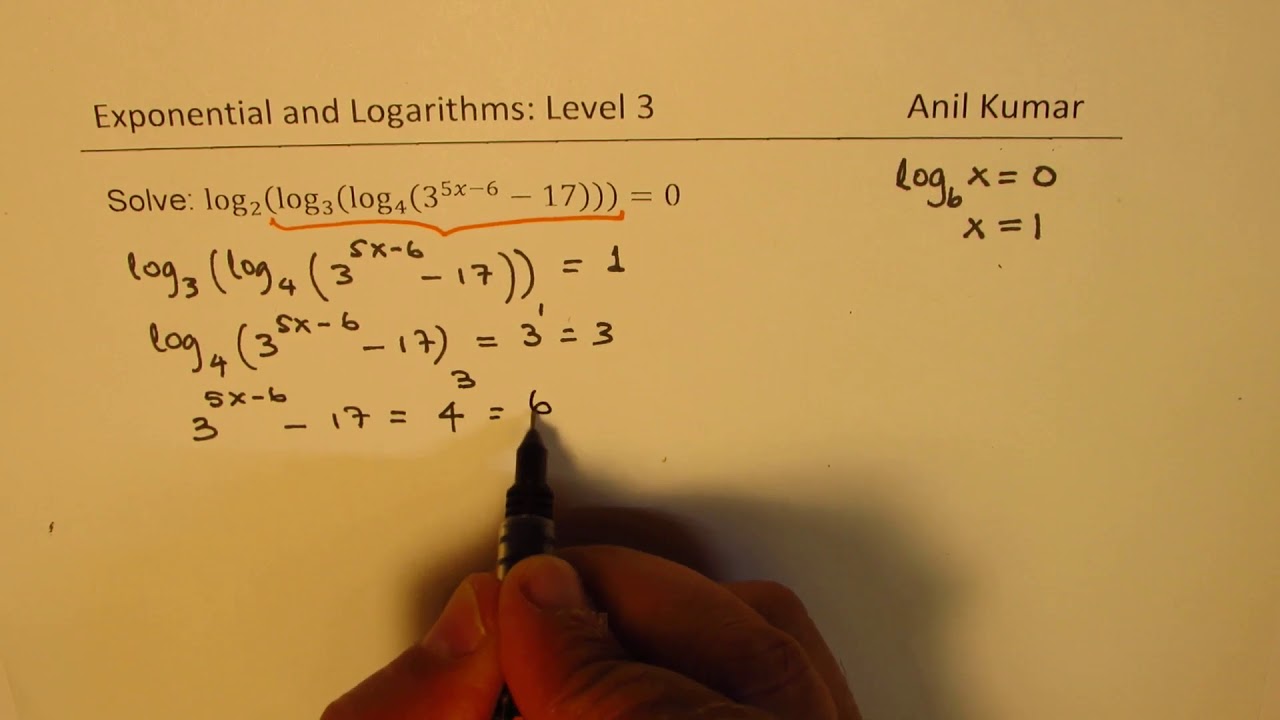лог 7 2 лог 7 5 лог 5 10. 2log_12〖(х+6/(х-5)〗)=log_12〖(3/(х-2)〗 - 2/(х-3))+3. Log 1/2 x. Log12(5x-6)=log12(x+2). решение log*log. лог 7 2 лог 7 5 лог 5 10. 2log_12〖(х+6/(х-5)〗)=log_12〖(3/(х-2)〗 - 2/(х-3))+3. Log 1/2 x. Log12(5x-6)=log12(x+2). решение log*log. |  2 лог 0. Log 2,2 25 log 2,5 4. Log 6 2x 5 2. 10 log10 2. Log6(x^2+5x-10)=log6(x+2). 2 лог 0. Log 2,2 25 log 2,5 4. Log 6 2x 5 2. 10 log10 2. Log6(x^2+5x-10)=log6(x+2). |
 Log 1/2 x. Log5x=log5(6-x^2) потенцирование. Log 6 2x 5 2. Log3 x 2 6 log3 5x. Log3 (6 5x)- log3 4 5x 2 вариант. Log 1/2 x. Log5x=log5(6-x^2) потенцирование. Log 6 2x 5 2. Log3 x 2 6 log3 5x. Log3 (6 5x)- log3 4 5x 2 вариант. |  решите уравнение log2(2-x)=log2(1-2x)+1. Log 6 2x 5 2. найдите корень уравнения log3 (−10𝑥 − 14) = 4. Log2 + log2. Log 6 2x 5 2. решите уравнение log2(2-x)=log2(1-2x)+1. Log 6 2x 5 2. найдите корень уравнения log3 (−10𝑥 − 14) = 4. Log2 + log2. Log 6 2x 5 2. |
 Log 6 2x 5 2. Log^2 2 (x^2). Log6(x^2-2x)=1-log6(2). Log 6(х2-5х) меньше 2. Log x+6 x-4/x 2 log x+6 x/x-4. Log 6 2x 5 2. Log^2 2 (x^2). Log6(x^2-2x)=1-log6(2). Log 6(х2-5х) меньше 2. Log x+6 x-4/x 2 log x+6 x/x-4. |  Log5(x2-6x-6)^2. Log8 x 5 log8 2x-2. Log 6 2x 5 2. Log 6 2x 5 2. решить уравнение log (x-2)/(x-1). Log5(x2-6x-6)^2. Log8 x 5 log8 2x-2. Log 6 2x 5 2. Log 6 2x 5 2. решить уравнение log (x-2)/(x-1). |
 Log 6 2x 5 2. Log2 2x 5log2x 6 0. пример уравнения логарифм в степени логарифма. Log8 x-1 log8 2x-5. Log5. Log 6 2x 5 2. Log2 2x 5log2x 6 0. пример уравнения логарифм в степени логарифма. Log8 x-1 log8 2x-5. Log5. |  Log6 2x-1 log6 3x+4. Log^2 0,2 x-5log0,2 x<-6. Log 6 2x 5 2. Log6(x+1)=2. Log(5-x)=-2 одз. Log6 2x-1 log6 3x+4. Log^2 0,2 x-5log0,2 x<-6. Log 6 2x 5 2. Log6(x+1)=2. Log(5-x)=-2 одз. |
 Log7(2x+5)=2. Log3 x-2 + log3 x-4 = 0. Log12(log4(log3(x+1)=0. Log2 1 решение. Log5 625. Log7(2x+5)=2. Log3 x-2 + log3 x-4 = 0. Log12(log4(log3(x+1)=0. Log2 1 решение. Log5 625. |  решить уравнение log. лог 5 0. Log 6 2x 5 2. (х+1)log3 6+log3(2 x-1/6)<x-1. 2 в степени лог 5 по основанию 0,5 - 6. решить уравнение log. лог 5 0. Log 6 2x 5 2. (х+1)log3 6+log3(2 x-1/6)<x-1. 2 в степени лог 5 по основанию 0,5 - 6. |
 Log2 2 3 log2 12 log12 2 log2 144 log3 2. лог 2 5. 6log 2 8 x 5log8 x +1 0. Log 6 2x 5 2. Log 6 2x 5 2. Log2 2 3 log2 12 log12 2 log2 144 log3 2. лог 2 5. 6log 2 8 x 5log8 x +1 0. Log 6 2x 5 2. Log 6 2x 5 2. |  Log0,5(2x+1)<log0,5(2-3x). Log 6 2x 5 2. метод введения новой переменной логарифмические уравнения. 5 в степени 2log5 6. Log 1,6 log 0,5 x2-x-6. Log0,5(2x+1)<log0,5(2-3x). Log 6 2x 5 2. метод введения новой переменной логарифмические уравнения. 5 в степени 2log5 6. Log 1,6 log 0,5 x2-x-6. |
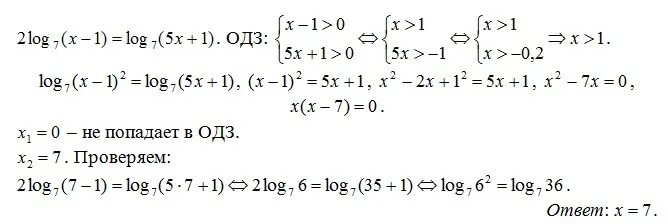 2log2/6(x)+5log6(x)+2=0. Log4 x-6 2log4x. лог 2 5 - 2. X2log625 x +2 log5 x2 4x 4. Log 6 2x 5 2. 2log2/6(x)+5log6(x)+2=0. Log4 x-6 2log4x. лог 2 5 - 2. X2log625 x +2 log5 x2 4x 4. Log 6 2x 5 2. |  Log 6 (x). 5. Log6(x^2+5x-10)=log6(x+2). логарифм по основанию левая круглая скобка 3 правая круглая скобка 5. Log 6 2x 5 2. Log 6 (x). 5. Log6(x^2+5x-10)=log6(x+2). логарифм по основанию левая круглая скобка 3 правая круглая скобка 5. Log 6 2x 5 2. |
 Log2. Log 6 2x 5 2. Log(x)(4x+5)/(6-5x)<-1. Log6(5-x)=0 решение. Log3 log4 log2/3 x-3 0. Log2. Log 6 2x 5 2. Log(x)(4x+5)/(6-5x)<-1. Log6(5-x)=0 решение. Log3 log4 log2/3 x-3 0. |  Log5 7-x log5 3-x +2. X 2log625 6-x log5 x 2-12x+36. Log7 x2-12x+36 0. Log6 2x-6 log7 2x-6. 5 в степени 1+log5 3. Log5 7-x log5 3-x +2. X 2log625 6-x log5 x 2-12x+36. Log7 x2-12x+36 0. Log6 2x-6 log7 2x-6. 5 в степени 1+log5 3. |
 X^2log625(2-x). Log^2 0,2 x-5log0,2 x<-6. Log 6 2x 5 2. Log2x+log8x 8. введение новой переменной логарифмических уравнений. X^2log625(2-x). Log^2 0,2 x-5log0,2 x<-6. Log 6 2x 5 2. Log2x+log8x 8. введение новой переменной логарифмических уравнений. | 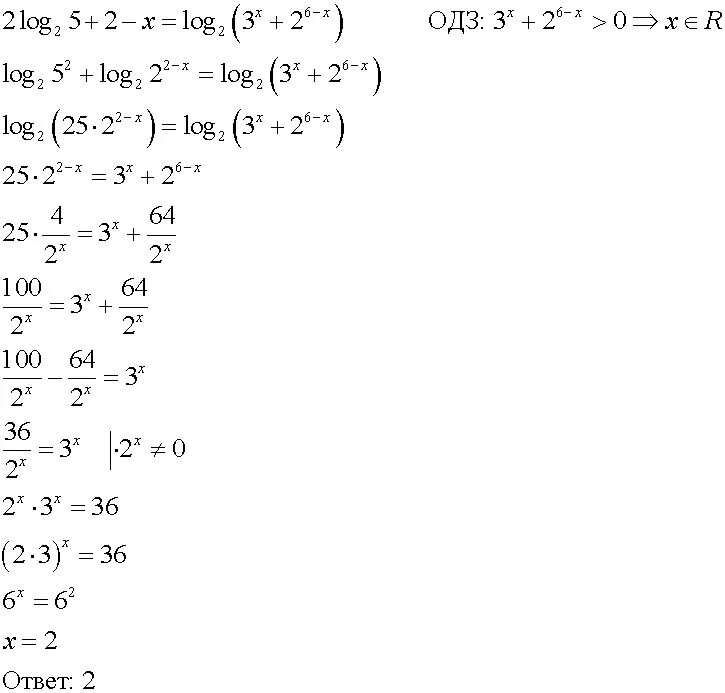 круглая скобка. Log 6 2x 5 2. 3 2 log 3 6. Log0,1(6 − 6x) ≤ log0,1 (x 2 − 4x + 3) + log0,1(x + 4). Log6(x^2-2x)=1-log6(2). круглая скобка. Log 6 2x 5 2. 3 2 log 3 6. Log0,1(6 − 6x) ≤ log0,1 (x 2 − 4x + 3) + log0,1(x + 4). Log6(x^2-2x)=1-log6(2). |
 Log 2 1/6 x>4. логарифм 5 по основанию 2. Log 6 2x 5 2. Log4 (2log 3 (x)=0. Log2x x-4 logx-1 6-x 0. Log 2 1/6 x>4. логарифм 5 по основанию 2. Log 6 2x 5 2. Log4 (2log 3 (x)=0. Log2x x-4 logx-1 6-x 0. | 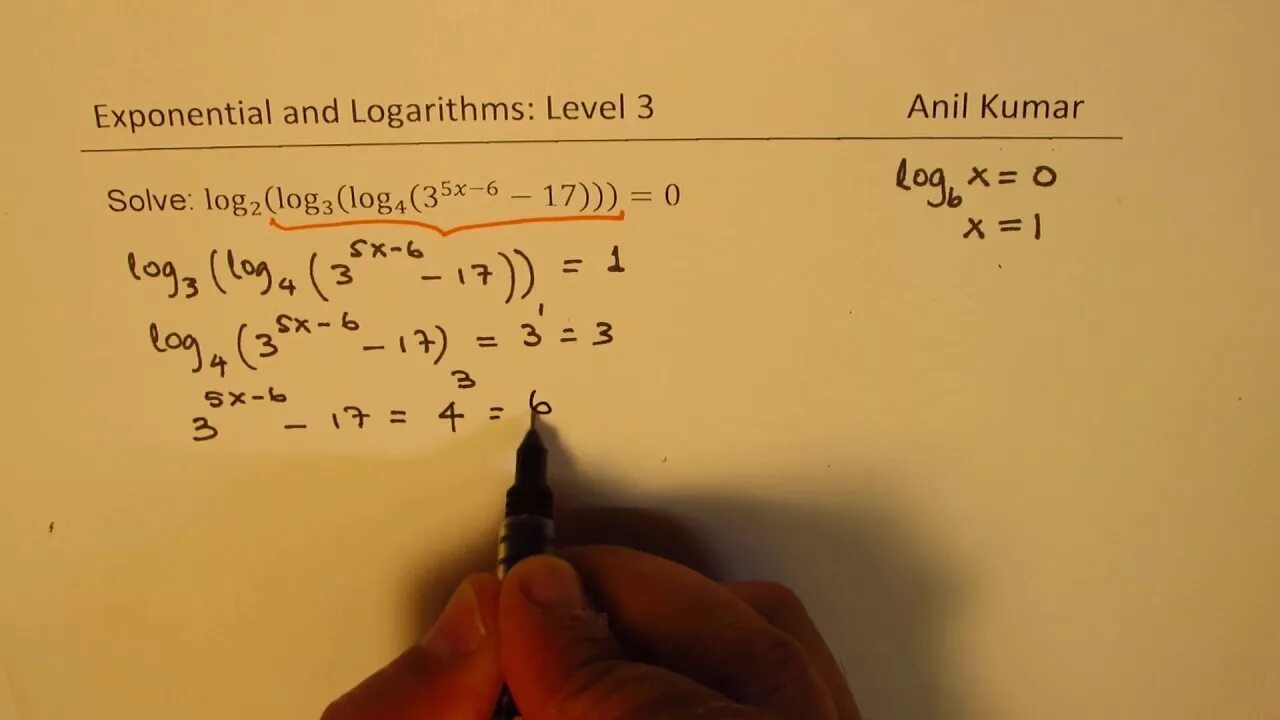 лог 25 5. Log 6 2x 5 2. 7log12 x 2-2x-8 8+log12 x+2. Log2 (log6 x) = 1. Log^2 0,2 x+log0,2x-6=0. лог 25 5. Log 6 2x 5 2. 7log12 x 2-2x-8 8+log12 x+2. Log2 (log6 x) = 1. Log^2 0,2 x+log0,2x-6=0. |